SGD와 같이 1차 미분을 통한 최저점을 찾는 방법에 대해서는
성능이 느리다는 단점이 있습니다.
지그재그로 경사를 내려가며 최저점을 찾기 때문에,
매우 속도가 느린 것이지요.
그 것의 대안으로 2차 미분을 이용한 최적화 방법이 있습니다.
2차 미분은 아래 그림의 빨간선과같이
더 빠른 최저점을 찾아갈 수 있는 대안을 제시합니다.
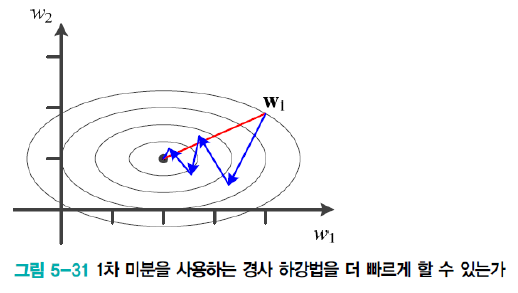
2차 미분을 활용하여, 매개변수를 업데이트 하는 수식은 아래와 같지요.

여기서 H(Hessian)은 2번 미분한 값입니다.
2차 미분의 가장 큰 단점은 아래와 같습니다.
1. 과다한 계산량 필요
2. 2차 미분이 불가능한 수식들이 존재
이 문제점을 해결하기 위해,
켤레그레디언트 방법과 유사뉴턴 방법이 등장했습니다.

왼쪽 그림은 SGD방법이고 오른쪽은 켤레그레디언트 방법입니다.
SGD방법에서 w1, w2, w3... 을 따라가보면
지그재그로 이동하는 것을 알 수 있습니다.
반면 오른쪽 그림은 w1시점에서 g1방향으로 이동하고,
최저점에서 다시 g2방향으로 이동하기 전에,
g1의 방향을 기억하고 초록색 선으로 수정하는 것입니다.
즉, 다시 말하면 켤레그레디언트 방법은
직전에 사용한 방향(pt-1)을 기억하여 다음 순간(pt)에
(pt-1과 pt)의 conjugate(켤레 쌍)을 활용하는 것입니다.
그 다음은 유사뉴턴 방법입니다.
유사뉴턴방법은 H(Hessian)을 구하기가 어려우니,
그에 근사한 값은 M을 구하여 사용하는 것입니다.
처음에는 단위행렬 I로 시작하여 그레디언트 정보를 이용하여
점점 H에 근사하는 M을 찾아나가는 방법입니다.
'IT > 머신러닝(수업)' 카테고리의 다른 글
| RBM과 DBN (0) | 2021.12.12 |
|---|---|
| 오토 인코더 (0) | 2021.11.25 |
| 규제 기법2 - Augmentation, Dropout, 앙상블 (0) | 2021.11.21 |
| 규제 기법 - Ridge & Lasso (0) | 2021.11.20 |
| 배치 정규화 (0) | 2021.11.15 |