다양한 그래프의 종류
1. directed/undirected graph
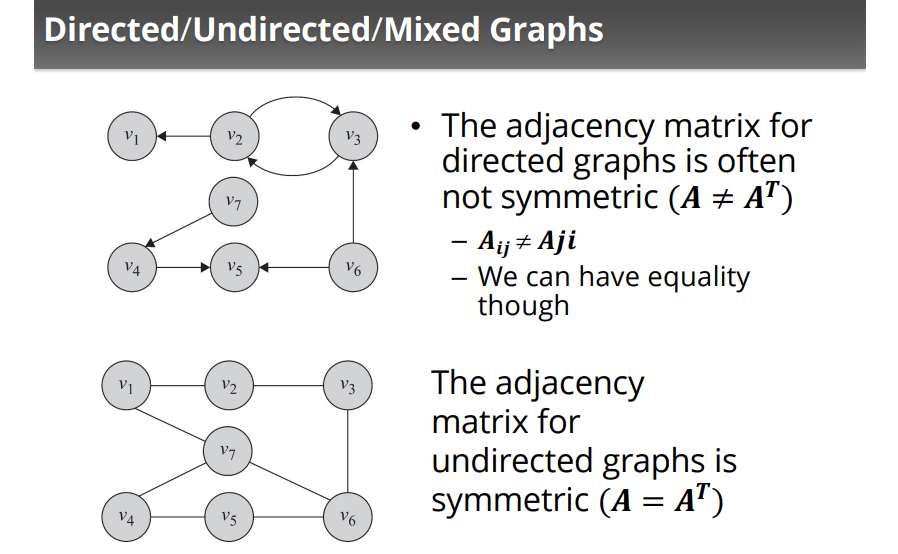
2. null / empty graph
null graph: 노드와 edge모두 0인 그래프
empty graph: 노드만 있고 edge가 없는 그래프
empty graph ⊃ null graph
3. simple graph/multigraph

4. webgraph
directed multigraph로 보통 webgraph를 표현
5. signed graph
foes or friends 관계를 표현할 수 있음 ( or social status)

그래프 관련 용어정리
incident하다라는 표현은
두 edge가 하나의 endpoint를 공유하고 있을 때

또한 방향성이 있는 edge라면 그 방향성도 같을 때,
incident 하다고 할 수 있다.
walk: a sequence of incident edges visited one after another
- open walk: 출발점과 도착점이 다를 경우
- closed walk: 출발점과 도착점이 같을 경우
walk를 표현할 때는,
edge로 표현하거나(e1, e2, ....)
node로 표현할 수 있음(n1, n2, ....)
** the length of walk = the # of visited edges
trail: walk의 한 종류이나, edge를 중복방문하지 않은 것
(edge를 중복방문하지 않는)closed trail=tour=circuit
path: walk의 한 종류이나, node와 edge를 중복방문하지 않은 것
closed path=cycle
length of path = 방문한 edge의 개수
아래 그림에서 v2 or v5까지만 간것이 path이고,
v6까지 가게 되면 trail이 된다.

Eulerian Tour

Himiltonian cycle

random walk: 다음 node를 임의로 선택하는 walk
확률을 사용해 다음으로 이동할 node의 가중치를 줄 수 있다.
(가중치의 총합은 1이여야 함)
connectivity: 인접(adjacent)해 있거나, vi -> vj로 갈수있는 edge가 있을 때
graph is connected: 모든 그래프가 연결 되어있는 경우
1. 방향성이 없는 그래프는 항상 연결되어있다고 할 수있다.
--> 아래 그림에서, 어떤 2개의 노드를 꺼내도 연결되어 있기 때문에
(항상 subgraph가 존재함)

directed/undirected graph의 특징들
1. undirected graph에서 subgraph는 각 노드별 어떤 조합을 만들어도 path가 존재한다.
2. directed graph에서 u부터 v까지 그리고 v부터 u까지 path가 존재하면
그것은 strongly connected component이다.
2. 방향성이 있는 그래프
(c)strongly connected: 어떤 두 노드를 꺼내더라도 양방향 연결 할 수 있음(양방향으로 이동 가능함)
(d)weakly connected: v3에서 v1으로 가는 연결edge를 찾을 수 없음
단, 방향성을 무시한 경우는 연결할 수 있는 경우를 weakly connected라고 함

n-hop neighborhood
v3기준 1-hop neighborhood는 v6이고
2-hop neighborhood는 v8이다.

diameter: 그래프의 지름은 임의의 2개의 노드를 선택했을때 가장 긴 path
--> the length of the longest shortes path between any pair of nodes


(diameter for web = 19 : 평균적으로 19개의 링크를 통해 데이터를 크롤링해오면
대충 모든 정보를 가져올 수 있다고 함)

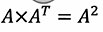
두 노드 사이의 공통된 neighbor의 개수를 의미
A^3: 3개의 노드사이에 공통된 neighbor 개수를 의미
tree: undirect and no cycle
아래의 왼쪽 그래프는 트리이고, 오른쪽 그래프는 트리가 아님(cycle이 존재하므로)

트리는 두 노드사이에 path는 오직 1개만 존재함.
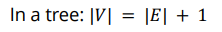
트리에서 edge+1= node의 개수임
spanning tree: tree의 모든 노드를 다 통과하는 subtree이며
아래 그림에서는 빨간선을 따라가는 spanning tree의 예시를 보여준다.
(여러개의 spanning tree가 존재 할 수 있음)

weight가 있는 경우, 최소의 weight를 가지는 spanning tree를 찾는 것이 중요함
MST: minimum spanning tree
steiner tree:

일부 노드를 연결하는데, 가장 최소의 weight로 연결하는 tree
complete graph:
굉장히 dense가 높은 graph로써 모든 node가 그래프로 연결되어있는 것
아래 수식은 connection의 개수를 의미하고
V의 노드가 n이라고 하면 connection의 개수는 nC2로 n(n-1)/2로 표현할 수 있음
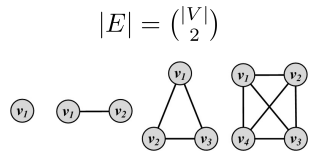
complete graph에서 각node의 degree는 모든 노드 -1
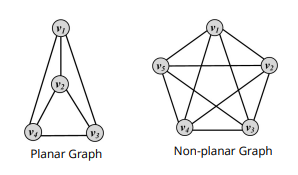
planar graph: 교차(cross)하는 그래프가 없는 것
bipartite graph
왼쪽 노드는 왼쪽노드끼리 연결된것이 아니라,
오른쪽과만 연결되어있는 것

bipartite graph는 affiliation network(소속 네트워크)에 주로 사용됨

아래와 같은 행렬로도 affiliation network를 표현할 수 있음

카일은 book club과 food bank에 속해있으므로 첫 행이 둘다 1,1임
- what is XX(T)? similarity between users (Bibliographic coupling)
사용 유저간의 유사도
ex) XX(T)의 (0,1)은 Kyle와 Kate가 같이 속하는 그룹이 1개가 있다는 뜻임
(0,0)은 Kyle이 2개의 그룹에 속해있음을 뜻함
| 2 | 1 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
- what is X(T)X? similarity between groups (co-citation)
(0,1) 은 Book club과 food bank에 공통으로 속하는 사람은 1명임
(0,0) 은 Book club에 속하는 사람은 Kyle과 Kate두명임
| B | F | |
| B | 2 | 1 |
| F | 1 | 2 |
Regular graph:
• A regular graph is one in which all nodes have the same degree

complete graph는 regular graph의 특징을 가지고 있다.
regular graph ⊃ complete graph
Egocentric network(그냥 읽어보기)
다른 노드와의 연결에는 제한이 있고 특정 노드와만 연결 되어있는 것
Usually there are limitations for nodes to connect to other nodes or have relation with other nodes
– Example: In a network of mothers and their children:
Each mother only holds mother-children relations with her own children
Bridges(cut-edge)
두 그룹을 연결하는 연결다리
아래 그림에서 굵은 검은 색 선

참고로 모든 그래프는 dmml.asu.edu/smm에서 볼 수 있으며,
서강대학교 social media data 수업을 정리한 내용입니다.
'IT > SNS분석' 카테고리의 다른 글
| Network models1 - real world network 특징 (0) | 2022.05.02 |
|---|---|
| [SNS analysis]Network measures2 (0) | 2022.04.12 |
| Network measures 1 (2) | 2022.03.29 |
| Graph algorithms (0) | 2022.03.22 |
| [SNS analysis] 그래프 관련 기본 개념 (0) | 2022.03.08 |