오늘은 pca, pls, tsne 등 다양한 차원축소 method중에
tsne에 대해서 정리해보려고 합니다.
한글로는 티스네라고 읽어요!
pca와는 조금 다르게,
tsne는 원래 데이터 형태가 곡선을 나타내는 모형일 때 더 성능이 좋아요.

보통 숫자 분류 mnist 데이터 셋에 대해 차원 축소를 고려하신다면,
0이나 8같은 숫자들은 곡선들로 이루어져 있죠.
이럴 때 tsne를 사용하면 더 성능이 좋다고 합니다.
반면에, pca는 feature들이 선형적 관계들이 있을 때 잘 분류하지요.
그래서 pca를 쓸 지, tsne를 쓸 지를 판단하시기 위해서는
가지고 있는 데이터들이 어떤 분포를 가지는지를 먼저 파악하는 것이
무엇보다 중요하지요.
또 pca는 skit-learn에서 decomposition로 불러오는 반면에
tsne는 manifold로 import 해온 답니다.
여기까지 tsne와 pca를 비교하는 내용은 마치고!
tsne를 어떻게 활용하는지 알아보기로 하죠.
|
1
2
3
|
from sklearn.preprocessing import minmax_scale
from sklearn.manifold import TSNE
|
cs |
우선 위에와 같이 필요한 라이브러리를 불러옵니다.
차원축소를 할 때는, 데이터들을 정규화 시켜 주는게 중요해요.
서로의 스케일이 다른 상태에서 바로 차원 축소를 해준다면,
큰 숫자의 범위를 가지는 feature의 중요도가
작은 숫자의 범위를 갖는 feature보다 더 의미있게 나타날 수 있기 때문이죠.
라이브러리를 불러왔다면 이제 데이터를 전처리하고,
전처리한 데이터로 tsne함수에 넣어주면 됩니다.
|
1
2
|
sm_scaled = minmax_scale(sm, axis = 0)
new_tsne=TSNE(n_components=2, random_state=1 , perplexity=30).fit_transform(sm_scaled)
|
cs |
튜닝 파라미터들에대해서 간략히 설명해 보자면,
우선 n_components는 몇차원으로 축소시킬 것이냐에 대한 값을 넣어주면 됩니다.
저는 2차원으로 축소시킨 뒤,
그래프를 그려줄 예정이라 2라는 값을 넣었어요.
ramdom_state는 1로 고정해서,
다시 돌리더라도 같은 결과값을 가질 수 있도록 해주죠.
그리고, perplexity는 그림보다는 그래프를 보면서 설명하는 게 더 좋으니
뒤에서 다시 설명하도록 하죠.
우선 위의 코드를 돌리면
new_tsne라는 값에는 아래와 같은 값의 쌍이 여러개 들어가있어요.
[0.209842723, 0.2817232]
|
1
2
3
4
5
|
x_val = new_tsne[:,0]
y_val = new_tsne[:,1]
plt.scatter(x_val ,y_val )
plt.show()
|
cs |
그래프는 위와 같이 간단히 그릴 수 있어요.
>> output
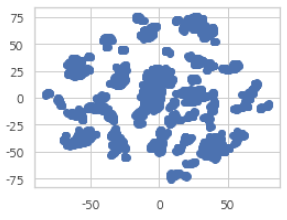
tsne는 위와 같이 간단히 결과를 낼 수 있습니다.
그럼!!
아까 얘기한대로, perplexity의 값은 무엇을 뜻하냐를 보기로 하죠.
아래와 같이 비교한다면 더 이해가 쉬울 거에요.

위의 그림처럼, perplexity값이 커질 수록 클러스터의 개수가 줄어들고,
각 클러스터의 사이즈가 커지는 것을 볼 수 있어요.
참고로, perplexity의 default값은 30입니다.
그리고 van der Maaten & Hinton에 따르면 가장 적합한
perplexity의 값은 5~50 사이라고 합니다.
너무 값이 작거나(5미만) 너무 크다면(50초과) 기존 분포와는 다른 분포를
나타낼 가능성이 많다고 해요!
또, n_iter라는 값이 있는데 이 값은 iteration을 몇 번 돌린 뒤
결과를 볼 것이냐에 대한 설정값인데, 최소 250이상으로 정해주면 됩니다.
아래 사이트는 tsne를 돌리기 전에 읽어보면
엄청 유익한 글이라,!!
꼭 읽어보시길 추천 드립니다.
distill.pub/2016/misread-tsne/
How to Use t-SNE Effectively
Although extremely useful for visualizing high-dimensional data, t-SNE plots can sometimes be mysterious or misleading.
distill.pub
'IT > 파이썬' 카테고리의 다른 글
| Bayesian optimization (0) | 2021.06.29 |
|---|---|
| [for loop 활용] 최적화된 feature set 찾기 (0) | 2021.06.25 |
| autogluon으로 최적화 모델링 만들기 (0) | 2021.04.23 |
| autogluon 설치 에러 이슈 해결방법 (0) | 2021.04.22 |
| 선형보간법(interpolation)으로 결측치 채우기 (0) | 2021.04.21 |