Information diffusion: 정보들이 확산되고 각각의 individual에 도달하는 것을 말한다.
3가지 요소
1. sender: diffusion의 시작
2. receiver: 정보를 받는 node
- receiver는 sender보다 보통 더 큼
- receiver에는 sender도 포함될 수 있음(정보로 전달하면서 받을 수 있음)
3. medium: 정보의 diffusion이 일어나는 매개체
Information Diffusion Types

Network observability: network의 실체가 관측 가능여부에 따라 Explicit/Implicit로 나뉨
Information Availability:
- global
- local
간섭 intervention:
delaying: 정보 확산을 지연시키는 간섭
expediting: 정보 확산 촉진
stopping: 정보확산 차단
Herd Behavior
• Network is observable
• Only public information is available
individual이 다른 객체의 decision에 따라 결정을 내리는 것임
complete graph와 유사함
(왜냐하면 public information을 공유하고, 다른 노드들을 관찰할 수 있기 때문)
eg)
online 경매 - 참가자들의 bidding, 참여도, 물건의 인기도 등을 알 수 있음
인기있는 레스토랑의 정보
Milgram's experiment: 3명이 한곳을 쳐다보며 다른사람도 따라서 쳐다 봄
Herd behavior의 2가지 구성요소
1. connections between individuals
2. method (정보 전달 매개체)
Designing a Herd Behavior Experiment
- decision을 내려야 하는 상황을 제공
- decision이 sequential order를 가짐
- 사람들이 의사결정하기 위해 개인적 정보를 활용함
- 개인적인 정보가 전달(no passing)되는 것이 아니라,(추측, 관찰) 그냥 global하게 주어짐
Urn experiment (Herding)
- 각 학생은 바구니에서 꺼낸 공의 색깔을 확인(자기만)
- 학생은 각 바구니의 majority color에 대해 추측한 결과를 칠판에 작성
- 앞에 blue, blue라고 적혀져 있는데, 내가 red공을 꺼낸다면
그래도 blue가 majority color가 블루라고 생각할 것임

Herding intervention:
private정보를 제공함으로써 기존 결과와 다른 결과를 초래할 수 있음

Information Cascade
정보들이 몇명의 user사이에서 전달되며
- 개인은 network로 연결되어있음
- 각각의 neighbor를 통해서만 정보가 확산됨
단 ,Cascade users have less information available
( 주어진 정보가 그렇게 많지는 않음 - herd의 global info와의 차이점 )
2가지 node종류가 있음
- active: 정보를 다른 이웃에게 전달하는 node
- inactive: 정보를 다른 이웃에게 전달X node
active → inactive (변환가능)
inactive → active (변환불가능)
Independent Cascade Model (ICM)
- Sender-centric model of cascade
- 딱 한번만 이웃노드를 활성화 시킬 수 있음 (활성화시킨다: 이웃에게 정보를 전달함)
- 노드가 활성화되는 것은 확률에 따름

초기 스타트 node를 최소화 하면서 (초기비용 최소화)
빠르게 정보를 확산 시킬 수 있는 방법을 알아내는데에 사용할 수 있음
Maximizing the spread of cascades
spread를 최대로 하는 가장 작은 starting set of node를 찾는 것임
starting node(S로표기)에 개수에 따라 cost(B로표기)가 결정됨 (비례관계)
f(S): S의 starting node로 부터 얻는 모든 spread node set
f(S)의 특징
1. non-negative
2. monotone
f(S+v) >= f(S) S에 새로운 v를 추가하면 더 큰 spread node set이 됨
3. submodular
N = {n1, ...., n10}
T = {n4, n5, n6, n7}
S = {n5, n6}
N/T = {n1, n2, n3, n8, n9, n10} 라고 할 때,
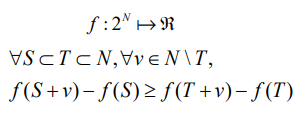
S는 T보다 적은 노드 set인데, 거기에 하나를 추가하는 것이
많은 노드 set에서 신규 node를 추가하는 것보다
information spread 효과가 더 크다는 의미임
Maximizing the spread of cascades의 장단점
단점: NP-hard 문제, 최적화된 정답을 찾는 것이 불가능함
node가 많으면 많을 수록 시간, 연산 많이 소요
장점: greedy algorithm을 사용해서 어느정도(63%) maximizing 된 결과를 찾을 수 있음
greedy algorithm (중요)!!
S에 노드를 한개씩 추가하면서 계산 하는 방법임

f(1)={1, 6, 4, 2} = 4
f(2) = 1
f(3) = 1
f(4) = 2
f(5) = 1
f(6) = 4
f(1)과 f(6) 둘 다 4이므로 둘 중 아무거나 선택해서 진행함
f(6,3) = 5
f(6,5) = 5
f(1)을 선택해도 동일함
f(1,3) = 5 = f(1,5)
'IT > SNS분석' 카테고리의 다른 글
| community evolution & evaluation (0) | 2022.06.07 |
|---|---|
| community analysis 3 (0) | 2022.05.31 |
| community analysis 2 (0) | 2022.05.24 |
| community analysis 1 (0) | 2022.05.17 |
| Classification with Network Information (0) | 2022.05.10 |