퍼셉트론 학습이란?
훈련집합이 주어졌을 때, 옳게 분류하는 퍼셉트론 (weight, bias)를 찾는 것
input layer, output layer 2개만 있음
입력층: d+1 (bias포함) 노드
출력층: 1개 노드 (2 class 분류기 일때)
이 외에도, 가중치 & 활성 함수 필요
아래 내용 풀어보기

패턴 인식에서 일반적인 학습 알고리즘 설계 과정
단계 1: 분류기 구조 정의와 분류 과정의 수학식 정의
단계 2: 분류기 품질 측정용 비용함수 J(Θ) 정의
단계 3: J(Θ)를 최적화하는 Θ를 찾는 알고리즘 설계
목적함수
분류기 품질을 측정하는 것

오분류라면 true answer와 prediction의 부호가 다르게 되고
위의 목적함수에서 보다시피 두 값을 곱하게 되면
오분류의 경우 항상 음의 값이 나옴
이것을 방지하기 위해 앞에 마이너스를 곱해줌
그러므로

목적함수의 특징 4가지

Gradient descent method
- J(Θ) = 0 인 Θ값을 찾는 것
- learning rate를 곱해서 조금씩 이동하면 좋음

iterative method를 통해서 J(Θ) = 0 인 Θ값을 찾게되면
local minima에 빠질 위험을 염두해 둬야 함
→ local minima에 빠지지 않기위해 초기값을 여러개를 두고 실험해야함
알고리즘에 필요한 수식들

식 4.5는 J(θ)를 w에 대해 미분, b에 대해 미분해서 나온 값임
위의 가중치 업데이트 방법을 퍼세트론 학습규칙이라 함
a를 분류하는 알고리즘에서 가중치 갱신하는 process

w(0), b(0)은 초기값임 - random하게 설정 함

1번에서 가중치 update를 통해 2번으로 갱신되는 과정을 보여 줌
** learning rate는 해에 접근할 수록 점점 더 작은 값을 취해주는 게 좋음
** 초기값은 random하게 선택하는게 좋음
퍼셉트론 학습: 배치모드 vs. 패턴모드
배치모드: 오분류된 샘플을 수집한 뒤 한꺼번에 가중치를 update 해주는 것 (주로 사용)
패턴모드: 오분류된 sample이 발생할 경우 바로 가중치를 update해줌
→ single sample perceptron이라고도 함
포켓알고리즘
: 선형 분리 불가능한 상황
J(Θ)=0이라는 목표를 버리고, J(Θ)를 최소화하는 목표로 수정


여기서 정인식률q = 품질은 accuracy와 같다고 생각하면 됨
perceptron의 한계(선형분리 불가능)를 극복하기 위한 방법
두 단계에 걸쳐 문제를 해결
1. 원래 특징공간을 새로운 공간으로 매핑
2. 새로운 공간에서 분류
아래 표가 다층 퍼셉트론을 표로 나타낸 것임

위의 표는 아래의 퍼셉트론 3개를 거쳐서 만들 수 있음

각 layer에 기호 정리

출력층 = O
전방 계산(foward computation)
위의 network를 수식으로 표현하면 아래와 같음

활성함수 (activation function)
a값에 따라 기울기가 변화됨

시그모이드 함수의 미분을 보면 원래 자기 값을 사용하는 것을 볼 수 있음
→ back propagation의 계산이 간단해질 수 있음
알파가 커질 수록 + 영역이 커짐

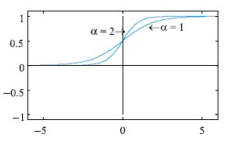
a가 커지면 위의식에서 기울기가 가파라지고
즉, activation이 많이 되는 것
즉, " + " 영역이 커진다는 것
MLP학습이란?
perceptron 학습에서 Hidden layer가 늘어난 것임
- 패턴 인식에서 일반적인 학습 알고리즘 설계 과정
단계 1: 분류기 구조 정의와 분류 과정의 수학식 정의
단계 2: 분류기 품질 측정용 비용함수(=목적함수) J(Θ) 정의

** 참고로, 제곱을 하는 이유는 양수화시키는 것과
추후 미분하기에 유리하기 때문
1/2를 곱해주는 것도 미분할때 상쇄시키기 위함임
단계 3: J(Θ)를 최적화하는 Θ를 찾는 알고리즘 설계
가중치 update 단계
1. 🛆(v) 업데이트

가중치 🛆(v)는 위와같이 업데이트 되는데
1. 여기서, δk의 수식을 보면
(실제 정답과 예측값의 차이 = error 값)(미분된값 = 기울기값)의 곱이므로
기울기가 크면 클수록, error값이 크면 클수록 업데이트 되는 양이 많아짐
2. z는 은닉층의 노드를 나타내는 것으로,
아래 그림에서 은닉층의 노드와 error값 포함값을 곱하여 가중치를 업데이트 함

2. 🛆(u) 업데이트

🛆(u) 를 계산 하기 위해서는 앞에서 발생한 에러(δ)를 포함하는り와
입력층 노드를 곱하여 업데이트 한다.
** 오류 역전파 알고리즘 수행 시,
batch size에 따라 수행이 되며 batch size가 train set만큼 커져서
train set이 weight를 update하는데에 모두 사용이 된다면 그걸 1 epoch이라 함
1번 batch하는것을 1 iteration하는 거임
train set이 k개의 batch로 나뉘면 k-iteration = 1 epoch
그러므로 전체 반복수는 k* # of epoch 임
학습 시 오류 역전파 알고리즘의 계산 복잡도
Θ((d+m)pHN)
d= depth (layer 개수)
m = 출력층 node의 개수
p = 은닉층 노드수
H = # of epoch
N = sample 수
많은 시간 소요
MLP 수행 시 시간 복잡도
Θ((d+m)p)
N에 무관, 빠름
4.3.4 구현과 몇 가지 부연설명
매개변수(hyper parameter) 설정
hyper parameter :
- layer 갯수, node 개수, tau값, batch size, batch normalization,
- kernel 개수, kernel size, pooling 방법 등이 포함됨
parameter : u, v값(가중치)
→ 파라미터설정은 transfer learning을 활용하여 할수도 있고
→ experimental, empirical(경험에의한)하게 hyperparameter를 설정함
'IT > 패턴인식' 카테고리의 다른 글
| 비선형 SVM (0) | 2022.11.17 |
|---|---|
| 선형 SVM (1) | 2022.11.09 |
| 확률 분포 추정 (0) | 2022.10.02 |
| 정규분포에서 베이시안 분류기 (0) | 2022.09.29 |
| Bayesian 결정이론 (1) | 2022.09.19 |