DQN이 등장하게된 배경
Q table로 해결하기 어려운 것
when the number of states is too large.
→ 계산하기가 매우 복잡해짐

위의 벽돌상태를 (깨진것, 안깨진것) 0,1로 표시하고 공의 위치를 0/1로 표시하면
너무 많은 조합이 있음
→ 해결책 ) 이미지 자체를 input으로 사용하자.
단, 순간의 이미지를 캡쳐하므로 공의 방향을 알기 어려움
→ 해결책 ) time-series 4개의 이미지를 연속해서 가져옴
하지만 또 너무 많은 조합
→ DQN을 사용하자.
DQN 정의: Q table을 함수화하여 input을 state로 정하고
output을 각 action에 대한 Q-value로 하는 것
Understanding DQN
- supervised learning을 사용함
- stochastic gradient descent 사용
- network에 batch of samples을 제공함
Training sample이란?
여러 episode를 실험하면서 얻은 transition (s, a, r, s') 들
reply buffer
실험 결과로 나온 transition을 저장하기 위한 buffer
→ 그때그때 transtion결과로 learning 하는 것이 아니라,
buffer에 쌓아놓은 뒤 한꺼번에 training을 시키는데에 사용함
Exprerience replay
reply buffer에 있는 것을 random으로 sampling 해서 training 시키는 것
loss function: MSE를 활용

K = batch size
yi = 정답
RL에서 정답이라 함은 Q*(S, a)이 정답으로 생각하고 RL을 수행함

따라서, 위의 MSE는 아래와 같이 표현할 수 있음

그래서 아래와 같은 loss function을 얻을 수 있음

next state가 terminal일 경우의 label 값은 아래와 같음
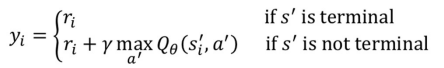
Loss function의 문제점 & 해결책: target network

정답 label도 θ에 영향을 받아 움직임
→ 안정적이지 못함
따라서, 정답 label은 100번중에 1번만 update시키는 방법으로 정함
→ target network를 사용함
if we freeze the target value for a while and compute only the predicted value
so that our predicted value matches the target value


아래코드에 대한 그림 설명

| s1 | s2 | s3 | s4 | ||||
| a | 1 | 0 | 1 | 1 |
s1일 때, 실제 값은 (0,1) = (0.8, 0.9)인데 여기서 max값인 0.9을 취하므로 s1일 때 action 1이 됨

terminal state경우, done_mask가 0이 되어 r값만 남게됨



DQN variation
1. Double DQN

정답레이블을 아래와 같이 사용하는 점이 바뀜
→ 가장 Q값을 높게하는 action을 사용하여 정답레이블을 정하는 것
→ 기존 label은 overestimate되어있다는 단점이 있음
(가장 높은 action의 q값이 원하는 방향이 아니더라도 무조건 사용하므로)
→ 즉, Because of this, the Q value is overestimated. In other words,
the Q value will be calculated larger than what it should be.

그러므로 위의 식에서는 gamma다음에 maxQ가 아니라, 그냥 Qθ'임
(괄호안에는 Qθ임)
→ 즉, Qθ'와 Qθ가 다른 θ를 가지므로, noise를 포함하여 어느정도 overestimate를 해결 했다고 할 수 있음
2. Dueling DQN
Deuling DQN 구조

Dueling DQN장점
V(s)가 network가 학습될 때마다 update되면서
더 빨리 정확한 값쪽으로 convergence 되도록 할 수 있음
(for better approximation of the state values)
Problem of identifiability
Q(s, a)는 V(s)와 Advantage function의 A(a)가 합쳐진 것이므로
둘중에 어느것이 적절하게 증가했는지 알기 어려움
(-1000+1060 = 60, 50+10=60)
해결책

위와 같은 방법으로 한쪽에 평균을 빼준 값과 더하여 Q(s,a)를 계산함

'IT > 강화학습' 카테고리의 다른 글
| Actor Critic methods - DDPG (0) | 2022.11.29 |
|---|---|
| Policy Gradient Methods (0) | 2022.11.15 |
| Temporal Difference Learning (0) | 2022.10.25 |
| Monte Carlo methods - Importance Sampling (0) | 2022.10.12 |
| Monte Carlo methods (0) | 2022.10.11 |