Chi-square test
category형 변수별 target 과의 유의차가 있는지 검정할 때,
Category변수가 많다면 아래와 같이 for문으로 작성하는 것이 더 편합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
from scipy.stats import chi2_contingency
chi_list=['cat1', 'cat2', 'cat3']
chi_val_list=[]
chi_p_list=[]
for i in chi_list:
# contingency: 관측도수
contingency= pd.crosstab(df[i], df['target'])
# dof: degree of freedom
# expected:
chi, p, dof, expected =chi2_contingency(contingency)
chi_val_list.append(chi)
chi_p_list.append(p)
|
cs |
아래와 같이 카이제곱검정의 결과를 Dataframe 화하여 간단히 분석 할 수 있습니다.
|
1
2
3
4
|
chi_frame={'chi': chi_val_list, 'p':chi_p_list}
chi_table=pd.DataFrame(chi_frame, index=chi_list)
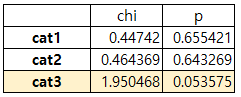
chi_table
|
cs |
[output]
Fisher's exact test
관측 도수가 5이하일 경우, 카이제곱 검정은 적용이 어려우니 아래와 같이 Fisher's exact검정을 활용합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
fisher_list=['small_cat1', 'small_cat2','small_cat3']
import scipy.stats as stats
f_val_list=[]
f_p_list=[]
for i in chi_list:
contingency= pd.crosstab(df3[i], df3['target4'])
f, p =stats.fisher_exact(contingency)
f_val_list.append(f)
f_p_list.append(p)
|
cs |
위에서와 동일하게 피셔의 정확성검정의 결과를 Dataframe 화하여 간단히 결과를 확인 할 수 있습니다.
|
1
2
|
f_frame={'f': f_val_list, 'p':f_p_list}
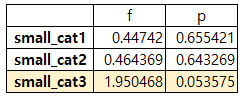
pd.DataFrame(f_frame, index=fisher_list)
|
cs |
[output]
Post-hoc
컬럼 small_cat3을 4개 category(3/5/10/20)를 가진 변수라고 할 때, 과연 어느 category끼리의 유의차가 존재하는지를 파악해 보는 작업을 하겠습니다.
|
1
2
3
4
|
from itertools import combinations
contigency= pd.crosstab(df['cat3'], df['target'])
all_combinations = list(combinations(contigency.index, 2))
all_combinations
|
cs |
all_combinations의 결과는 아래와 같지요.
[(3.0, 5.0), (3.0, 10.0), (3.0, 20.0), (5.0, 10.0), (5.0, 20.0), (10.0, 20.0)]
총 4개의 값이었으니, 모든 조합은 6에요.
그러면 그 모든 조합에 대해서 fisher's exact test의 사후검정을 진행해볼게요.
|
1
2
3
4
5
6
|
for comb in all_combinations:
# subset df into a dataframe containing only the pair "comb"
new_df = contigency[(contigency.index == comb[0]) | (contigency.index == comb[1])]
# running chi2 test
chi2, p = fisher_exact(new_df)
print(f"Chi2 result for pair {comb}: {chi2}, p-value: {p}")
|
cs |
[output]
Chi2 result for pair (3.0, 5.0): 12.083333333333334, p-value: 8.699334452113366e-06
Chi2 result for pair (3.0, 10.0): 6.258503401360544, p-value: 0.002284940290099475
Chi2 result for pair (3.0, 20.0): 10.980392156862745, p-value: 0.000173366953300
Chi2 result for pair (5.0, 10.0): 0.517945109078114, p-value: 0.07636422839592397
Chi2 result for pair (5.0, 20.0): 0.9087221095334685, p-value: 1.0
Chi2 result for pair (10.0, 20.0): 1.7544757033248082, p-value: 0.2632132888509211
즉, small_cat3변수에서 3이라는 클래스는 다른 모든 클래스(5, 10, 20)과 유의차가 있는 class라고 확인할 수 있겠습니다.
'IT > 파이썬' 카테고리의 다른 글
| GridSearchCV 그리드서치 1탄 (0) | 2020.12.21 |
|---|---|
| 의사결정나무(Decision Tree) 그래프 그리기 (0) | 2020.12.10 |
| Imbalanced Dataset에서의 over sampling과 cross validation (0) | 2020.12.09 |
| ANOVA분석 & POST-HOC (사후검정) (0) | 2020.12.04 |
| T-Test, levene test, 맨-휘트니 U 검정(Mann-Whitney U test) (0) | 2020.12.04 |