1. 5가지의 activation function에 대한 정리
a. Step Function

이제는 거의 사용하지 않음
b. Sigmoid Function


Gradient Descent가 발생할 수 있음
c. tanh function

sigmoid는 0~1값을 갖지만, tanh는 -1~1의 값을 가지므로 변화폭이 더 큼
그러므로 sigmoid 함수보다는 기울기 소실이 적은 편임
d. ReLU

f(x) = max(0, x)
tanh과 같이 연산이 필요한 것이 아니라, 단순 임계값이므로 연산속도가 빠름
e. Leaky ReLU
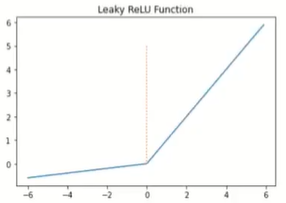
f(x) = max(ax, x)
a는 일반적으로 0.01값을 가짐
f. softmax function

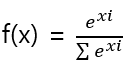
2. 7가지의 Optimizer 방법
optimizer의 전체 흐름은 아래 표에 잘 정리되어있어서 가져온 것

a. Batch Gradient Descent (BGD)
- 단점: 큰 메모리가 필요하며, 시간이 오래걸림
- 장점: Global minimum에 빠질 가능성이 없음
b. Stochastic Gradient Descent (SGD: 확률적 경사하강법)
- BGD와의 차이: 매개변수 값을 조정 시, 전체 데이터가 아닌, 랜덤으로 선택한 하나의 데이터에 대해서만 계산함
- 단점: BGD보다 정확도가 낮고, 매개변수의 변경폭이 불안정함
- 장점: 속도가 BGD보다 빠름
c. Mini Batch Gradient Descent (가장 많이 사용)
- BGD, SGD와의 차이: 전체 데이터도 아니고, 1개의 데이터도 아니고 정해진 양에 대해서만 계산함
- 장점: BGD보다 빠르며, SGD보다 안정적임
d. 모멘텀
SGD에 관성(v)을 더해준 것임
- θ = θ + v
- v = αv - pg
- ∴ θ = θ + αv - pg
여기서 α는 0.5, 0.9, 0.99을 주로 사용하며,
α=1에 가까울 수록, 이전 그레디언트 정보에 큰 가중치를 주는 셈이다.
코드: keras.optimizers.SGD(lr=0.01, momentum = 0.9)
d-1. 네스테로프 모멘텀
현재의 관성(v)값으로 다음 이동할 곳의 θ ̃를 예측하고
그 그레디언트를 사용


e. AdaGrad
이전 기법과 달리, 각 매개변수에 서로 다른 학습률을 적용시킴
이때, 변화가 많은 매개변수는 학습률을 작게 설정
왜냐하면, 많이 업데이트 된 가중치는 최적값에 충분히 가까워졌을 수 있기 때문임
단, 업데이트가 많아도 가까워지지 못한 가중치가 있을 수 있어서, AdaGrad방법은 잘 사용하지 않음

-> r 은 이전 gradient를 누적한 벡터
코드: kears.optimizers.Adagrad( lr=0.01, epsilon=0.00006)
단점: 계속 학습을 진행할 수록 학습률이 지나치게 떨어짐
f. RMSProp
Adagrad의 단점 개선
AdaGrad에서는 단순히 제곱을 더하는 수식임 ( g⊙g )
따라서, " r " 이 무한이 커지는 AdaGrad의 단점을 막기위해,
매 업데이트마다 이전의 r 을 일정비율로 줄여줌 (가중 이동 평균 기법 적용)

여기서 α 는 0.1, 0.01, 0.001을 사용하며,
α가 작을 수록 최근것 ( g⊙g )에 비중을 더 둔다는 것임
코드: keras.optimizer.RMSprop( lr=0.01, rho=0.9, epsilon=0.00006)
g. Adam
스텝 방향의 조절과, 스텝 사이즈의 조절을 합친 것으로
제일 많이 사용함
코드: keras.optimizers.Adam( lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0, amsgrad=False)
'IT > 머신러닝(수업)' 카테고리의 다른 글
| 배치 정규화 (0) | 2021.11.15 |
|---|---|
| 가중치 초기값- He, Xavier initialization (0) | 2021.11.14 |
| 로그우도 목적 함수와 multi-class classification (0) | 2021.10.08 |
| 교차엔트로피 목점함수와 Binary classification (0) | 2021.09.30 |
| 목적함수에 대한 정리 (0) | 2021.09.29 |