가중치 초기값
이번에는 가중치 초기값의 2가지 규칙과
초기화 기법 2가지 방법을 알아보겠습니다.
가중치 초기값에서는 아래의 2개의 규칙만 기억해주면 됩니다.
1. 가능하면 작은 값의 가중치를 사용
(단, 가중치 값들이 동일한 값을 갖으면 안됨)
2. 각 층의 활성화 함수를 거쳐 나온 값들은 적당히 골고루 분포되어있어야 함
2번 규칙을 조금 더 자세히 알아보도록 하죠.
아래 그림은 w값이 평균 0, 표준편차 1인 정규분포에서 초기화 시킨 후,
sigmoid 활성화 함수를 거쳐 나온 값입니다.

결론을 말하면 위의 출력값들은 좋지 못한 값을 가지고 있습니다.
왜냐하면,
sigmoid출력값이 0과 1에 치우쳐져 있기 때문에,
back propagation을 진행하게 되면
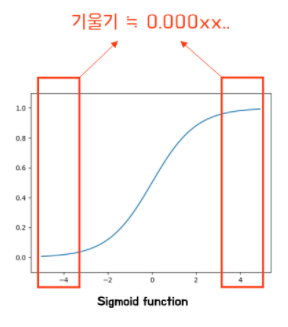
아래 그림과 같이 sigmoid함수에서 양 극단의 값의 기울기는 0이되는
vanishing gradient문제가 발생하기 때문입니다.
w의 표준편차가 더 커지면 커질 수록
vanishing gradient문제는 더 많이 발생할 것입니다.
그렇다면, 이번엔 w를 초기화 시킬 때,
평균 0, 표준편차 0.01로 작은 표준편차를 갖게 해보겠습니다.

vanishing gradient문제는 해결 되었지만,
출력값이 치우쳐져 있다는 문제점이 있습니다.
따라서, 적당히 골고루 분포되어있게 만들어 주는 것이 중요합니다.
그때 사용하는 기법이 아래와 같이 2가지 방법이 있습니다.
- Xavier initialization
- He initialization
1. Xavier initialization

주로 sigmoid, tanh와 같은 S자형 곡선을 갖는 활성화 함수와 같이 쓰임.
즉, 뉴런의 개수가 많아지면 그 만큼 적은 값의 분포를 활용하는 것입니다.
2. He initialization

ReLU와 주로 같이 쓰임.
'IT > 머신러닝(수업)' 카테고리의 다른 글
| 규제 기법 - Ridge & Lasso (0) | 2021.11.20 |
|---|---|
| 배치 정규화 (0) | 2021.11.15 |
| 6가지의 activation function과 7가지의 optimizer (0) | 2021.10.25 |
| 로그우도 목적 함수와 multi-class classification (0) | 2021.10.08 |
| 교차엔트로피 목점함수와 Binary classification (0) | 2021.09.30 |