가장 좋은 slot machine을 찾기위해 아래와 같은 프로세스를 따름

- 모든 slot machine을 실험해보고
- 그중에서 가장 max의 reward를 주는 slot machine을 찾음
이 실험을 위해 발생한 비용을 regret이라고 함
즉, regret = cost
multi-armed bandit에서의
- action = slot machine arm의 개수 = number of bandit
- observation space= 1
(왜냐 하면 slot machine을 땡기면 매번 똑같은 state로 돌아오기 때문에)
- p_dist = 각 slot machine(기계)의 승률
- r_dist = reward distribution = (1, 1, 1) → 이기면 1, 아니면 0
multi-armed bandit의 전략
코드와 전략 mapping 하기(시험)
- epsilon-greedy
- softmax exploration
- upper confidence bound (UCB)
- Thompson sampling
Epsilon greedy
epsilon으로 가끔 exploration을 하지만 주로, 좋은 결과를 가져오는 것으로 선택하는 것

Q = 61/75
Softmax exploration
기존 epsilon greedy단점은 모든 machine의 arm을 동일한 횟수로 돌려보지 않는 것임
즉, 1등인 애는 많이 기회를 얻으나, 2등, 3등, 4등은 epsilon에 따라 random으로 선택하므로,
2등과 나머지를 다 동일하게 여기는 것이 문제임
softmax function을 이용한 확률값을 나머지 등수에게 적용함

여기서 T를 높이면 거의 유사한 확률로 적용이 되나,
T를 낮추면 유사하지 않은 확률로 적용이 됨
ex) T가 크면
| 점수 | 100 | 90 | 80 | 70 |
| 적용 확률 | 0.26 | 0.255 | 0.24 | … |
ex) T가 낮으면
| 점수 | 100 | 90 | 80 | 70 |
| 적용 확률 | 0.99 | 0.005 | 0.0024 | … |

denom = 분모(denominator)라는 뜻임
Upper confidence bound (UCB) = optimism
In UCB, we always select the arm that has the high upper confidence bound.

초기에 가능성이 커보이는 Upper가 높은(upper bound) arm1을 먼저 땡기고

여러 번 반복하면 신뢰구간이 줄어들어 의사결정을 할 수 있음

→ N(a)가 높아지면, 즉 arm을 땡기는 횟수가 많아지면 UCB는 줄어듬
왜냐하면 UCB는 신뢰구간이므로 신뢰구간이 축소되는 것임 (mean값으로 모임)

Thompson Sampling: based on a beta distribution.
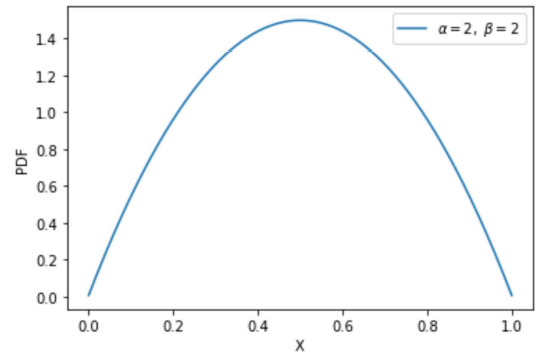
x라는 random variable을 뽑을 probability distribution function에서 a=b일 때 위와 같은 모양이 나옴

a, b의 값에 따라 위와 같은 그래프로 표현이 됨
초기 a=b인 상태에서 arm1를 땡겼을 때 이기면 arm1의 a를 +1 해주고, arm2가 지면 arm2의 b에 +1 해줘서 각각의 분포에 수렴에 가는 것을 뜻함
(교재 그림 참고)

'IT > 강화학습' 카테고리의 다른 글
| Proximal Policy Optimization (PPO) (0) | 2022.12.13 |
|---|---|
| Twin Delayed DDPG (TD3), Soft Actor-Critic (SAC) (2) | 2022.12.06 |
| Actor Critic methods - DDPG (0) | 2022.11.29 |
| Policy Gradient Methods (0) | 2022.11.15 |
| Deep Q Network (0) | 2022.11.01 |