Three spectral analysis techniques
1. FFT: contiunous spectrum을 contiunuous wave form으로 바꾸는 것
FFT를 하기위해 2의 지수승으로 바꿔야 됨(0으로 padding함)
그러면 DFT 보다 빠르게 처리할 수 있어서 Fast Fourier transform이라고 함
참고) DFT란? (Discrete Fourier transform)
입력 신호(wave form)를 디지털 신호로 바꾸는 것(=DFT)은 아래와 같음
1. sampling 함
2. sample을 discrete하게 변환하는 것임
2. LPC (linear predictive coding)
filter의 coefficient를 분석하는 것 (vocal tract의 coefficient를 분석해서 인식하는 것)
입력신호의 msg정보를 추출하는 것임
단, noise에 취약하다는 단점이 있음
3. Cepstral (or homomorphic) analysis
스피커에 대한 정보를 버리고 msg에 대한 정보만 취하는 것
Pattern matching
1. DTW (dynamic time warping)
발음의 길이가 다르므로 spectral distance를 metric형태로 분석
"ㅊ", "ㅣ", "ㄹ" 각각 길이가 다름
2. HMM (hidden Markov model)
Front ends: Mel cepstrum, PLP, delta cepstral coefficients
Mel cepstrum : Non-uniform한 bin으로 쪼개는 방법을 사용하는 cepstrum
PLP: 귀가 처리를 하는 방식을 모사해서 perceptual(인식) mechanism을 LPC에 추가한 것임
delta cepstral coefficients: 이웃한 frame의 시간차를 계산하여 보는 것
ASR: Automatic speech recognition이 어려운 이유
1. 음성은 continuous하기 때문 (연음현상 포함)
2. 사람마다 발음, 말의 속도가 다름
3. vocabulary size 매우 큼(신조어 추가)
4. 배경소음, 스피커와 화자사이의 위치에 따라 음성이 왜곡되는 것( = channel charateristics),
마이크 품질, 공간에 대한 영향등을 고려해야 함
ASR에서 고려해야 하는 것
1. Speaker dependent or speaker independent
2. Isolated speech, continuous speech, or keywords 중 어떤 것에 대한 인식인지
(keyword: 원하는 keyword가 문장내에 있는지 알아내는 것)
3. Lexicon (=발음 사전, vocabulary) size
4. Perplexity (문법등의 복잡도)
5. Speaking style(발표문 또는 일상대화 인지)
6. Recording conditions(sampling rate이 얼마인지)
Components of ASR
1. input acquisition (화자, 방음상태, 소음등)
2. front end(signal processing and feature selection)
3. local match: distance를 계산
4. Global decoder: Time align(시작시간 맞추기)
5. Language model
Euler’s FORMULA

위의 식을 증명하면

Fourier Series(for 주기신호) and Fourier Transform(for 비주기신호)
Fourier series (for a periodic signal)
Fourier transform (for a non-periodic signal)
주기신호일 때, Fourier Series적용하는 방법
Fourier Analysis: time domain → 주파수 도메인으로 변경하는 것
Fourier Synthesis: spectrum → time domain으로 복원하는 것

왼쪽 하단의 1번은 아래쪽과같이 여러개의 wave를 합치면 점점 비슷하게
square 신호 모양으로 합쳐진다 (하지만 완벽한 원복은 불가능함)
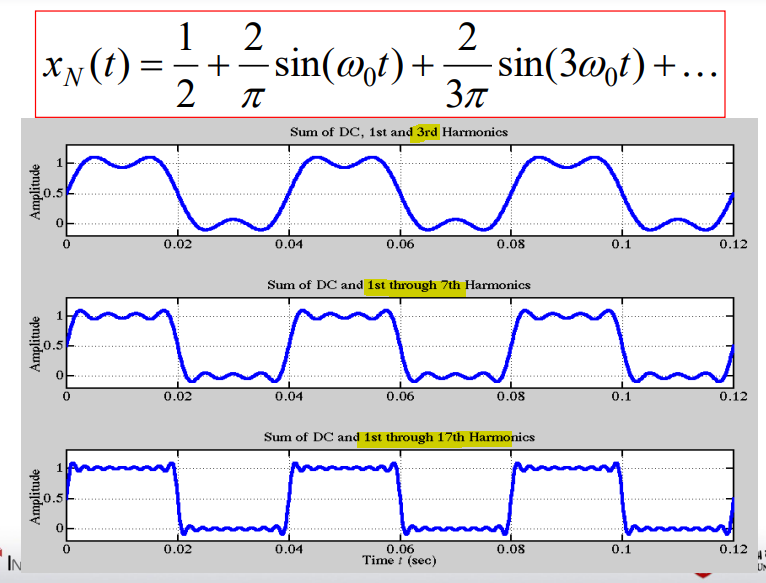
Fourier series의 기본 정의:
임의의 주기신호를 sinusoid의 합으로 나타낼 수 있다.
비주기신호일 때, Fourier Series적용하는 방법

주기 신호에서 주기를 무한대로 늘리면(아래로 내려갈 수록) 비주기 신호가 된다는 점을 착안함
이걸 spectrum으로 표현하면 descrete한 신호가 continuous한 신호로 변경됨

그러므로, T가 커질 수록 주파수(frequency)가 작아지는 것을 알 수 있음

Fourier Series vs. Fourier Transform
- Fourier series 의 spectrum은 discrete함
- Fourier Transform의 spectrum은 continuous한 frequency에 대해서 모든 지점의 값이 존재함
Discrete-Time Signals
sampling 목적: 디지털 컴퓨터로 처리하기위한 작업
1. sampling 작업을 함
x(t)의 input이 들어왔을 때 시간단위(T*delta(t))로 sampling 하는 것이고 수식은 아래와 같음
(sampling을 하면 주기성을 갖게됨)

아날로그 신호가 있을 때, uniform한 time interval을 가지고 sampling 하는 것임

2. Fourier transform을 적용함
Sampling Theorem (1): 정보손실이 없이 sampling 하는 것이 목적임
가장 높은 frequency가 정해져있을 때, (Fmax = B )
아래와 같은 rate로 sample 하면 정보손실이 없게 sampling(analog to digital)할 수 있음

(sampling frequency를 Bandwith의 2배 이상으로 해야된 다는 뜻임)
최소의 sampling rate을 Nyquist rate이라고 함

그리고 sampling된 것을 아래와 같은 수식으로 interpolation만 해주면 원상태로 복원할 수 있음

sampling frequency를 Bandwith의 2배 이상으로 해야된 다는 뜻은
너비가 Bandwith의 2배 이상이 되어야지 겹치지 않게 되고,
그러므로 완벽하게 복원할 수 있기 때문임

Discrete-Time Systems (1)
Discrete-Time signal(=input sequence)을 처리하기 위한 system
즉, input sequence → output sequence로 처리하는 시스템
가장 많이 사용하는 것은 LTI임
linear time-invariant (LTI) system
linear system이라 함은 아래 2조건을 만족하는 것임
1. homogeneity
입력을 임의의 상수배해서 transform하면 원래 신호에 대해 상수배하는 것과 같다

2. Superposition(중첩) principle

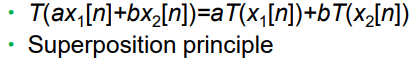
time invariant하다는것은 시간에 따라 system이 변하지 않는 다는 것임
input에서 delay가 일어나면 output에서도 delay가 일어나는 것
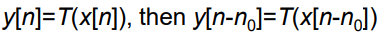
LTI 시스템의 가장 큰 특징
convlution으로 표현이 가능함


impulse response: impulse를 input으로 입력했을 때, 출력되는 signal sequence
convolution: impulse signal과 impulse response 만 가지고, output signal을 구하는 또다른 컴퓨팅 기법
시스템의 효용성을 판단하는 기준 2가지
1. BIBO stability: 입력이 bound되어있으면, 출력도 bound되어 있어야 함
(입출력이 유한하다는 뜻)
LTI system이 아래 조건을 만족하면 BIBO stability를 만족하는 것임

2. Causality
입력이 들어간 이후에만 출력이 나와야 함
LTI system이 아래 조건을 만족하면 Causality를 만족하는 것임
n<0일 때, 0이 되어야 함

참고하며 좋은 블로그입니다.
https://velog.io/@baeksh1997/%EC%9E%90%EB%8F%99%EC%A0%9C%EC%96%B4-Dynamic-Response
자동제어 - Dynamic Response
시스템이 어떻게 움직이는지를 알아보도록 하자학부 수준에서 제어공학이 잘 이루어 지려면 선형시스템에 대해서 많이 이야기 한다.입력에 $${\\alpha}$$배 만큼 키운 입력을 주었을 때 $${\\alpha}$$
velog.io
https://blog.naver.com/ptm0228/221848611209
신호와 시스템 - LTI System과 Convolution(Discrete)
이전시간에 설명했던 LTI System. Review : Impulse Representation LTI System에서 Discrete ...
blog.naver.com
'IT > 음성신호처리' 카테고리의 다른 글
| wave basic (0) | 2023.04.06 |
|---|---|
| LTI Systems과 여러종류의 digital filter (0) | 2023.03.30 |
| Discrete-Time Fourier Transform (DTFT) (0) | 2023.03.23 |
| z-Transform (0) | 2023.03.22 |
| 음성신호처리 개론 (0) | 2023.03.09 |