Properties of the DTFT
1. X(w) is complex : real + imaginary parts가 합쳐진 형태임
2. 2兀마다 주기성을 가짐
3. x[n]이라는 real sequence가 있을 때, conjugate symmetric한 관계임
(y축기준 좌우 대칭)

DTFT결과
DTFT를 취하면 왼쪽에서 오른쪽과 같이 변형됨을 알 수 있음

Frequency Response
전기 회로나 기계 진동계에 일정한 주파수의 입력을 가하였을 때 생기는 진동의 진폭이나 위상


첫번째 수식을 그림으로 표현하면 exponentialy decaying하는 함수로 표현할 수 있음
그 위의식에 노란색값을 곱한다는 의미는 x축으로 w0만큼 수평이동시킨다는 뜻임

Uncertainty Principle

주파수 domain에서 넓어지면 time domain 좁아지므로 time domain에서 resolution이 나빠짐
trade off 관계가 있다는 그림을 나타냄
이러한 trade off 관계를 uncertatinty principle이라고 함
Discrete-Time Systems에서 Frequency Response를 계산하는 방법
주파수 성분으로 쪼갠 뒤, 각 성분에 아래와 같은 빨간값을 곱하는 것과 같다.

1번은 입력신호, 2번은 출력신호
2번수식에서 입력신호값에 빨간밑줄이 곱해지므로 x축만큼 수평하게 이동하는것임
Convolution Theorem
time domain에서의 convolution이, 주파수 domain에서는 단순히 곱해지는 것임

Windowing (Modulation) Theorem
windowing 한다는 것은 수식으로는 특정 값을 곱하는 것임

즉, 아래그림에서 1번을 windowing하기위해 2번과 곱해줌
그 결과가 가장 아래쪽 3번째 줄에 나오는 response형태로 변형됨

하지만, 특정 windowing을 곱해줌으로써 에러가 발생할 수 밖에 없음
(노란색과같이 원래와 다른 형태임)
원래는 impulse형태였는데, 종모양으로 퍼지는 것이 에러가 더해진 것임
우리의 음성신호도 vocal tract을 거쳐 speech로 transform 되는데,
사람마다 다른 vocal tract이므로 에러가 포함되는 것이라고 생각하면 됨

windowing의 목적: time domain의 범위가 무한대 이므로, time domain에서의 범위를 줄이기 위함
즉, time domain에서의 resolution을 높이기 위함임
→ Uncertainty principle을 적용하면, 주파수 domain에서는 resolution이 나빠짐
Hamming Window
Impulse signal에 가장 효과적인 window 임
Discrete Fourier Transform(DFT)
DTFT의 단점) Fourier Transform결과물이 discrete함을 뜻함
→ 디지털 시스템에서 사용 불가
DTFT는 주파수 domain에서 continuous하므로, 주파수 domain에서 sampling을 하는 것이 DFT임

위의 수식은 DTFT의 수식인데, 이것을 유한한 영역(0~N-1)으로 한정 한것이 DFT임
* x[n], x[k]의 최대의 길이는 N과 같거나 작아야함
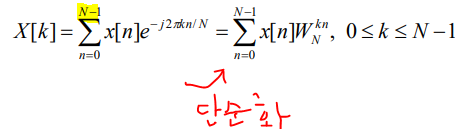
Sampling the DTFT
아래의 빨간색 밑줄은 노란색처럼 시차를 미뤄가며 누적시키는 것을 뜻함

x[n] is a length-M sequence일 때, y[n] = x[n] (출력 = 입력) 이 만족하려면
유한한 sequence여야 함( 0 ≤ n ≤ N-1)
** DTFT는 time domain에서 sampling 하는 것이므로, 주파수 domain에서 주기성이 생기고,
** DFT는 주파수 domain에서 sampling 하는 것이므로, time domain에서 주기성이 생김
참고) DFT assumes the implicit periodicity with period N (N의 주기성을 가짐)
수식으로는 아래와 같이 표현함
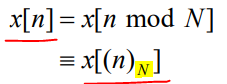
주기성을 가지므로 shift가 circular shift로 표현되어야 함
Shift → Circular shift
Circular shift

x[n-1]인 경우, 가장 왼쪽의 그림에서 가장 끝에있는거 앞으로 밀려가는 것을 뜻함
DFT 특징
time domain의 g & h, 주파수 domain의 G& H가 있을 때,
아래와 같은 특징을 가짐

Linear Convolution

n=2일때는 0*2 + 1*1 + 2*0이되는 것이고
n=0일 때는 x[0]h[0-0] + x[1]h[0-1] + x[2]h[0-2]가 되므로
한칸씩 밀려져서 곱하는 것 과 같음

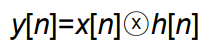
N=4일 때 위의 계산을 결과는 아래와 같이 2/2/3/2 임

2/2/3/2의 결과는 빨간색 표시처럼 중복된 곳을 더해준효과와 같음
overlap이 일어 발생하기 때문에 linear convolution과 circular convolution의 결과가 달라지게 됨
따라서 Linear convolution 길이를 제한함(아래내용 참고)
Linear convolution의 길이
M+L-1 <=N인 경우, linear convolution과 circular convolution의 결과가 같아짐

Fast Fourier Transform(FFT)
DFT의 복잡도 O(N*N) 임
더 간단히 할 수 있는 방법이 FFT이고
FFT의 복잡도는 (N/2)logN 으로 줄어들 수 있음. (단, N=2의 지수승일 때만 가능- 2, 4, 32 등..)
'IT > 음성신호처리' 카테고리의 다른 글
| wave basic (0) | 2023.04.06 |
|---|---|
| LTI Systems과 여러종류의 digital filter (0) | 2023.03.30 |
| z-Transform (0) | 2023.03.22 |
| 음성신호처리 개론2 (0) | 2023.03.16 |
| 음성신호처리 개론 (0) | 2023.03.09 |