LTI system: digital filter의 output임

Y(z)를 좌변으로 이동한다음에 X(z)로 나누면 H(z)를 얻을 수 있음
우변의 첫째항의 의미는 feedback항을 나타냄
Digital filter의 종류
- FIR Filters
- IIR Filters
- Linear Phase Filter
FIR Filters

LTI system과 달리 feedback항이 없음
아래와 같이 무한대로 더해나가는 구조임

장점1. stable함
장점2. have linear phase
(계산량이 충분할 때만 사용 가능함)
IIR Filters
무한히 더하는 형태가 아니라, feedback을 추가하는 것임
FIR Filters처럼 무한히 더한것이 아니라, feedback항을 추가하여 무한효과를 낼 수 있음
( impulse response 가 infinite함)

단점1. not have linear phase. (phase distortion발생)
단점2. unstable
stable하게 만들기위해서는 feedback loop를 잘 조절해야함
(파란색에서 곱해지는 값이 1보다 크게되면 무한히 큰값이 생성되므로
1보다 작은 값을 곱해줘야함 = Poles insde the unit circle)
> 단점이 불구하고도 IIR filter를 사용해야되는 필요성은
FIR filter는 frequency response가 좋지 않음
계산량이 너무 많은경우는 FIR보다는 IIR이 더 좋을 수 있음
Linear Phase Filter
w만큼 delay시키고, symmetry center의 위치를 M/2에 두는 것

Desired Frequency responses 종류 (ideal한 버전임, 실제 존재 X)
** O는 filter를 통해서 내보내는 영역임

Impulse response of the ideal lowpass filter(lowpass filter를 예로 듬)

하지만 practical하게 사용할 수 없음
일반적으로 practical하게 사용할 수 있는 filter는 아래와 같음

passband와 stopband사이를 딱 이분법적으로 끊어서 신호를 보내고 안보낼 수 있는게 아니라,
위의 그림 처럼 transition band구간의 누수가 발생함 (왜냐면 신호의 길이가 너무 길어서)
해결책) 실용적으로 사용할 수 있도록 window라는 기법을 사용함
> window는 성능이 좋지는 않지만 사용하기 쉬움
> Equiripple Linear-Phase FIR Filters
window종류 - 아래그림 참고
- Rectangular
- Bartlett (Triangular)
- Hanning(파란색구간은 뚝 떨어짐)
- Hamming

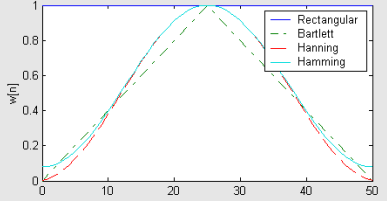
filter를 씌웠을 때 원하는 것은 신호가 들어오다가 뚝 끊기는 것인데,
아무리 window를 씌워도 완벽한 해결이 되지는 않음

주파수의 폭(Mainlobe width)이 좁고, 높이(Peak sidelobe)가 낮아야 되는데
bartlett은 폭이 너무 넓다는 단점,
rectangular는 높이가 높다는 단점
따라서 Hamming이 가장 좋은 window임.

Equiripple Linear-Phase FIR Filters 만들기
Linear-Phase한 FIR Filters
실제 신호가 H일때 D(desired amplitude response)를 빼준 것을 error라고 하고

** desired amplitude response: Lowpass, Highpass과 같이 ideal한 response
예를 들어, passband를 아래와 같은 point(fpts)에서 pass하게 만들면
▫ N = 26
▫ fpts = [0 0.25 0.3 0.5 0.55 1]
▫ mag = [0 0 1 1 0 0]
▫ Wt = [1 1 1] : weight
▫ h = firpm(N, fpts, mag, Wt)
아래와 같은 passband가 생성됨

equiripple하다는 것은 높이와 진폭을 동일하게 하는 것임 (stable함)

'IT > 음성신호처리' 카테고리의 다른 글
| speech production (0) | 2023.04.07 |
|---|---|
| wave basic (0) | 2023.04.06 |
| Discrete-Time Fourier Transform (DTFT) (0) | 2023.03.23 |
| z-Transform (0) | 2023.03.22 |
| 음성신호처리 개론2 (0) | 2023.03.16 |