주성분 분석 principal component analysis
Karhunen-Loeve (KL) 변환 또는 Hotelling 변환이라고도 부름
정보 손실을 최소화하는 조건에서 차원 축소
저차원으로 투영한다는 것의 의미

저차원으로 투영한 뒤에, 원래 점들을 구별할 수 없으면 좋은 차원축소X
(c)에서 가장 정보의 손실이 최소화되는 방향으로 저차원으로 축소한 것임
(c)가 변환된 공간에서의 분산이 가장 큼
정보손실
원래 훈련 집합이 가진 정보란 무엇일까?
샘플들 간의 거리 or 그들 간의 상대적인 위치 등
PCA는 샘플들이 원래 공간에 ‘퍼져있는 정도를’
변환된 공간에서 얼마나 잘 유지하느냐를 척도로 삼음
→ 이 척도는 변환된 공간에서 샘플들의 분산으로 측정함
→ 목표: 변환된 샘플들의 분산을 최대화하는 축을 찾는 것
분산 계산 예시)

분산을 가장 크게하는 축 찾기
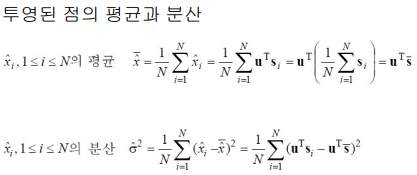
라그랑제 multiplier를 사용하여 최대화 하는 u를 찾으면 됨

위의식을 미분



위의 식의 의미는
훈련 집합의 공분산 행렬 Σ를 구하고,
그것의 고유 벡터를 구하면 그것이 바로 최대 분산을 갖는 u가 됨
공분산행렬 특징 참고

Eigen value(lambda), Eigen vector

고유값이 큰 순으로 d개의 Eigen vector만 골라서 PCA를 수행함
따라서 D 차원을 d 차원으로 줄인다면 고유값이 큰 순으로 d 개의 고유 벡터를취함.
PCA예제)
** 차원이 5이상이면 손으로 풀기 어려움

노란색은 원점에서 부터의 거리라고 할 수 있음
변환 행렬
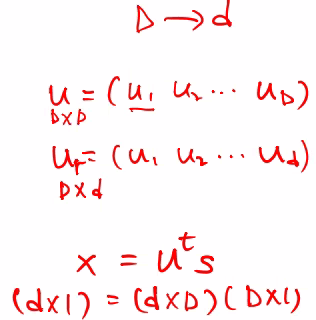
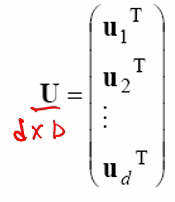
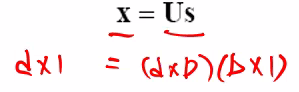
power 설명
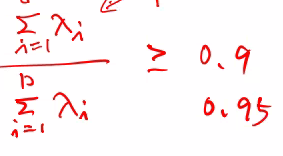
0.9, 0.95 power일 경우
D는 100차원이었는데, d(대략 10)차원으로 축소하여
90%정도의 설명력(power)를 갖는 것을 의미함
PCA 사례)
얼굴데이터를 차원축소함
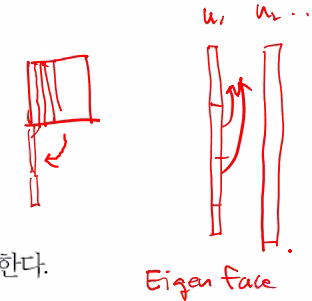
원래 n2차원을 1차원의 eigen vector로 표현한뒤
다시 n2차원으로 변형한것을 eigen face라 함
얼굴이라는 것은 어느정도 평균을 가지고 있는 데이터이기에
차원축소의 결과가 효과적임
Fisher의 선형 분별: Linear Discriminant Analysis (=LDA)
클래스 정보가 있을 때, 주로 사용
PCA와 Fisher LD 비교
차원을 축소한다는 것은 같지만 PCA와 Fisher LD는 목표가 다름
PCA는 정보 손실 최소화 (샘플의 부류 정보 사용 안함)
Fisher LD는 분별력을 최대화 (샘플의 부류 정보 사용함) - class 정보 활용
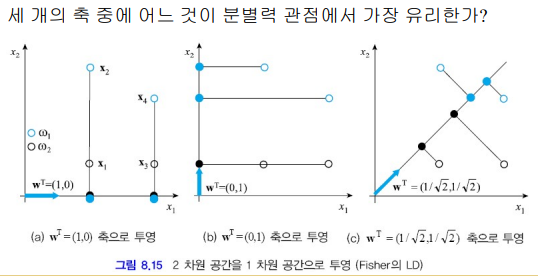
(b)가 가장 좋은 축임. 왜냐하면 파란점 검은색점이 잘 분류 되었으므로
PCA와 동일하게 평균, 분산을 먼저 구함
클래스 내의 평균:
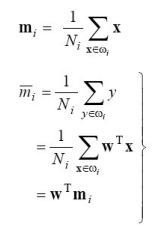
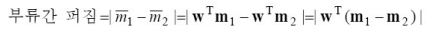
클래스 내의 분산:
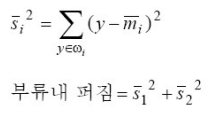
목적함수:

부류간 퍼짐between-class scatter (B)
부류내 퍼짐within-class scatter (w)

위의 값을 미분하면
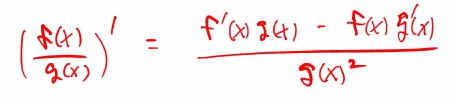
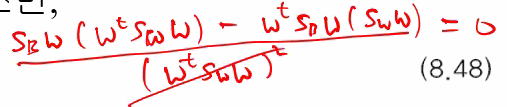

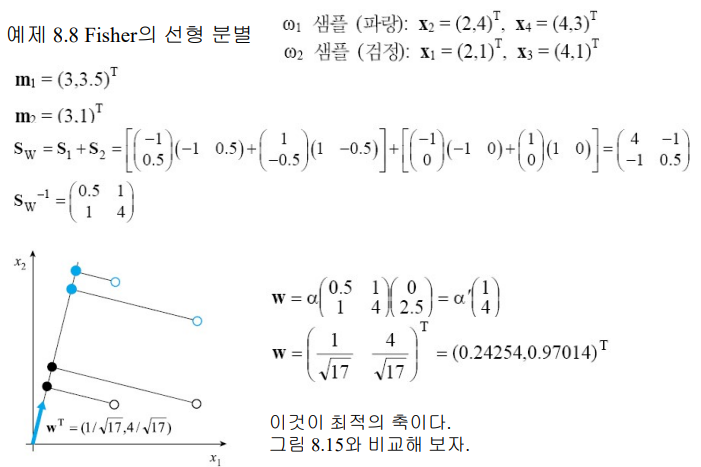
위의 결과를 활용한 예제)
특징추출의 실용적 관점
- 거리개념이 없다면(eg. 혈액형) one-hot벡터로 변환하여 특징을 추출함
- 특징마다 동적 범위가 크게 다르면?
: 특징값을 정규화 시켜서 사용함
