
nominal data(명칭)는 거리측정이 불가능함
distance metric
- 유클리디언 거리(L2-distance)

- 맨하탄 거리(L1-distance)
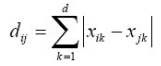
- Hamming 거리(이진 벡터에 적용 가능: 서로다른 비트의 개수)

- 코사인 유사도(문서 검색 응용에서 주로 사용)
작을 수록 similarity가 커지는 것임
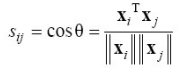
- 이진 특징 벡터의 유사도

점과 군집사이의 거리측정 1

점과 군집사이의 거리측정 2

아래 내용 시험!

두 군집 사이의 거리

동적거리 측정 방법
샘플마다 특징 벡터의 크기가 다른 경우
예) 온라인 필기 인식, DNA 열
(6.3 절의) 교정 거리 활용 = Levenshtein edit distance
군집화 알고리즘
계층 군집화: 군집 결과를 계층을 나타내는 덴드로그램으로 표현
분할 군집화: 각 샘플을 군집에 배정하는 연산 사용
신경망: SOM, ART
통계적 탐색: 시뮬레이티드 어닐링, 유전 알고리즘 등
계층 군집화:
a. 응집방식 bottom-up ↔ 분열 방식 top-down
샘플 각각이 군집이 되어 출발, 유사한 군집(D_min사용)을 모으는 작업을 반복
(덴드로그램 : duration이 긴쪽에서 잘라줌)

Dmin 사용하면 단일 연결single-linkage
Dmax 사용하면 완전 연결complete-linkage
Dave 사용하면 평균 연결average-linkage 알고리즘

군집 개수 알아내는 방법:
사용자가 지정 or 자동결정
- 단일 연결과 완전 연결은 외톨이에outlier 민감
- 평균 연결은 외톨이에 덜 민감
b. 분열 방식 top-down
모든 샘플이 하나의 군집으로 출발, 군집을 나누는 작업을 반복
분할 군집화
순차 알고리즘
- 특성
* 군집 개수를 찾아준다. (대신 임계값을 설정해주어야 한다.)
* 순서에 민감하다. 빠르다 (선형 시간).
k-means 알고리즘
- 특성
* 가장 널리 쓰인다.
* 군집 개수를 설정해주어야 한다.
- 이론적 배경
* (10.23)을 비용 함수로 하는 내리막 경사법의 일종
* 항상 지역 최적점으로 수렴한다. (전역 최적점 보장 못함)
* 초기 군집 중심에 민감
* 빠르다.
* 외톨이에 민감하다. (k-medoids는 덜 민감)
MST알고리즘
GMM 알고리즘
샘플로부터 가우시언을 추정하고 그 결과에 따라 군집 배정
- 가우시언 추정은 EM 알고리즘을 사용할 수 있다
신경망
sample과 weight 값의 거리를 구하여
가장 가까운 weight를 sample(입력특징벡터)과 유사한 값이 되도록 update함
그 결과, sample이 가장 가까운 노드와 연결되어 분류할 수 있음
SOM 학습 규칙: W_old는 x와 유사한 방향으로 update함

'IT > 패턴인식' 카테고리의 다른 글
| 특징 선택 (0) | 2022.12.14 |
|---|---|
| 특징추출2 - PCA, LDA (0) | 2022.12.08 |
| 특징추출 - 퓨리에 변환 (0) | 2022.12.07 |
| 순차데이터의 인식 (1) | 2022.12.01 |
| 질적 분류 (0) | 2022.11.24 |